克雷格·莱特亲自解密比特币密钥验证过程

”使用Jean-Paul Sartre来签名与使用Jean-Paul Sartre，诺贝尔奖获得者签名，意义是不一样的。

——Jean-Paul Sartre，1964”

我记得在多年以前读到了这句话，自此之后心里就感到不舒服。然而，在多年之后，在经历过这些年的大起大落之后，再回想起这句话的时候心中感到一片平静。使用Craig Wright签名与使用Craig Wright，中本聪来签名，意义是不一样的。

虽然我知道这是事实，但是我的内心并不希望如此。

IFdyaWdodCwgaXQgaXMgbm90IHRoZSBzYW1lIGFzIGlmIEkgc2lnbiBDcmFpZyBXcmlnaHQsIFNh

dG9zaGkuCgo=

我已经盯着屏幕看了好几个小时，但是仍旧无法寻得合适的词汇来表达内心深处对那些从最初就开始支持比特币的人的感激之情——人数太多以至于无法一一 列出。你们为了这个也许会一无所获的开源项目奉献了自己的青春与成果，多年来牺牲了人际关系和休息时间，而现在仍旧在为之奋斗拼搏。这个的社区的热情，智 慧和毅力已经传承了我的贡献，培养了它，拥抱了它，为它带来了生机。你们为这个世界带来了一份大礼，对此，我万分感谢。

放心，这些年来我也没有闲着。自从那时起，在与中本聪形象保持距离之后，我就将自己的所有努力都融入到研究当中去了。我保持着沉默，但是从未缺席比特币活动。我正与一个特殊的团体合作并且期待在合适的时机分享我们的成果。

中本聪已死。

但是这只是一个开端。

密钥验证

在本篇文章的其余部分，我将对密钥验证的过程进行解释。

为了确保我们能够正确使用 OpenSSL的椭圆曲线参数成功签署并验证消息，我们首先要确保成功加载secp256k1曲线。这在Centos Linux上并不是默认的。在此我就不详细叙述了。我要指出的是RPMForge对进行修补过的二进制文件进行维护。如果你是像我一样使用的是 Centos，我的建议就是从OpenSSL网站下载的源文件和补丁。

建议读者初步阅读以下的一些网站：

•https://wiki.openssl.org/index.php/Command_Line_Elliptic_Curve_Operations

•http://www.secg.org/sec2-v2.pdf

•https://www.openssl.org/

•https://www.bfccomputing.com/bitcoin-and-curve-secp256k1-on-fedora/

第一阶段将会解释一下哈希函数。在下图中我们展示了一个叫做“sn7-message.txt”的文件。

上图中呈现的一系列十六进制值代表着一个输入值的SHA256哈希。一种好的哈希算法将产生一大串不能够提前确定的值。信息的数量和排列的所有可能 性总是会超出模拟的范围，该模拟能够从任意的哈希函数中输出，但是总是会存在碰撞。鉴于技术的目前水平，要想找到一组输入值与同样的输出值产出碰撞的哈希 函数并不可行，而这一点却是能够确保哈希函数如SHA256的有用性和安全性。

SHA256算法提供的信息的最大量为(2^128−1)位同时返回32字节或256位作为输出值。能够输入 SHA256哈希函数的信息数量为(2^128−1)! 可能的输入值为从0位到上面指出的我们能够接受的最大范围。

在决定碰撞的可能范围的时候，我们有一个二项式系数(n)，该系数通过组合学决定了排列组合。

我将会在之后的文章中详细介绍有关冲突检出的数学问题。需要指出的是，虽然每一个哈希都有着惊人数量的碰撞值，但是找到两个碰撞值或者提前决定它们的概率可以说是无限小。

散列法

哈希函数相对简单并且用手就可以做到。当然这掩盖了哈希函数反向的复杂性。一种好的哈希函数简单易用，但是反向则不行。下图中显示了Linux哈希程序“sha256sum”的运行。该程序会返回一个对应着一组固定的输入的特殊值。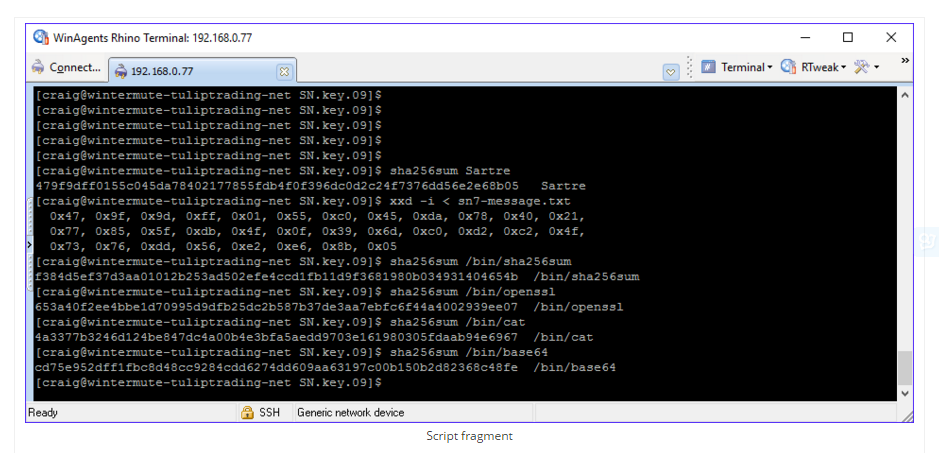

上图中，我们已经在几个文件上运行了该程序，其中一个文件我们正在OpenSSL签名中使用。这一特殊文件叫做Sartre。该文档的内容如下图所示：

数字签名算法签写了信息的哈希。虽然说也可以签下信息，但是如果签下哈希就可能确保信息的完整和验证信息是否出现变化。即便是一个空格或者一个句号被改变，该哈希就会与最初的返回值在根本上出现不同。

为了写入该值并将其存入文件中，我们可以使用Linux命令，xxd。这将把ASCII值写入一个十六进制二进制文件。输入下面的命令，我们可以在一个叫做“file.name”文件中写入一连串的0。

echo '000...000' | xxd -r -p > file.name

为此，我们可以改变收到的字符串作为从哈希算法到一个十六进制编码文件的输出。我们可以对这种信息进行签名和验证。对你加入到上面的echo命令中的字符串进行验证是很重要的。如果一个数位被打错，那么消息就不能进行验证。

公钥

为了验证一种数字签名消息，我们需要很多条件，包括：

•算法

•我们希望进行验证的签名方的公钥

•已经签名的消息

•数字签名文件

第一部分，需要的算法可以通过安装已经合并了secp256k1曲线补丁的OpenSSL来获得。以上步骤还包括创建一个散列信息。下一部分包括使用ECDSA公钥。

在这一步中，我使用了一个保存在 OpenSSL中的PEM文件中的公-私钥对，David Derosa已 经写了一个很好的页面来对 OpenSS椭圆曲线密钥对的创建进行定义。在上图中你可以看到特定的PEM格式公钥，该公钥与消息签名中使用的密钥对密切相 关。详细阅读David的页面可以为读者提供所有有关比特币交易中使用的私钥如何能够被格式化为PEM文件的详细信息。该页面中详细介绍了一个新的私钥的 创建而不是如何将现有的私钥导入到OpenSSL。我将介绍这一额外的过程并且演示一种基于椭圆曲线密码体制的现有私钥对如何能够被导入一种ASN.1格 式来与OpenSSL直接使用。

导出我们公钥的命令如下：

openssl ec -in sn-pub.pem -pubin -text -noout

0411db93e1dcdb8a016b49840f8c53

bc1eb68a382e97b1482ecad7b148a6

909a5cb2e0eaddfb84ccf9744464f8

2e160bfa9b8b64f9d4c03f999b8643

f656b412a3

这些返回字符串是程序使用的公钥值，包括比特币签名函数的验证和寻址。

Casascius已经开发了一种工具，可以帮助你解码公钥和返回有关的比特币地址，

签名

使用OpenSSL数字签名信息的过程需要信息签名方已经访问了私钥。最近几天，我已经使用了10中与比特币地址有关的私钥。这些都已经加载进 SPV钱包Electrum，其中我对一些信息进行签名，这些信息不是由我选择的而是由其他人选择的。在某些情况下，我们通过下载新版本的 Electrum来确保过程的完整。

我运行的electrum版本是Centos Linux v7，通过Python运行

签名验证

最后一步就是签名了。我们将会使用一下的命令将base64格式签名转换成一种能够加载进OpenSSL的文件格式。

>> base64 –decode signature > sig.asn1 & openssl dgst -verify sn-pub.pem -signature sig.asn1 sn7-message.txt

我们要进行验证的签名文件包括以下数据：

————————- Signature File ————————-

MEUCIQDBKn1Uly8m0UyzETObUSL4wYdBfd4ejvtoQfVcNCIK4AIgZmMsXNQWHvo6KDd2Tu6euEl1

3VTC3ihl6XUlhcU+fM4=

————————- End Signature ————————–

下图所示，我们展示出了该签名文件，在保存该文件时，你可以剪切和粘贴编码的签名并通过使用如Vim的编辑程序将它插入一个保存文件。

一些脚本

为了简化该程序，我已经纳入了两个shell脚本文件。有关这些脚本的变体，请访问网站如Enrico Zimuel的网站，这个网站不是特别专注于椭圆曲线密码学，但是更新其代码并用到基于比特币的系统上并不困难。

签名

为了让你可以在空闲的时候进行测试，我在下面包括了签名脚本。使用该脚本，输入包括变量<file>，该变量能够用来表示你期望使用被 选出来的<private_key>进行签名的文件。在该命令中，这个<private_key>变量代表着一个文件，该文件中 包含着用于消息签名的私钥。

EcDSA.Sign.sh <file> <private_key>

验证

我们可以使用一种相似的程序来验证我们创建的签名，使用以下的脚本。

EcDSA.Verify.sh <file> <signature> <public_key>

在该命令行中，变量<file>表示我们要进行验证的文件的名字。变量<signature> 代表我们保存签名（使用 Base64进行编码）的文件。最后一个变量<public_key> 包含PEM格式公钥。这些文件可以一起使用，如果都是有效并且正确 的，那么就可以成功地对数字签名进行验证。

选择格式

比特币使用的签名格式是基于DER编码的。在过去7年时间里，其他被应用于原始代码的方法已经出现了巨大变化。对签名和其他信息选择使用DER编码 是基于一种期望——确保信息能够在不兼容的系统之间进行共享。这并不是最高效的信息存储方式，但是它确实使完全不同的系统进行有效地交流。

与许多开源项目一样，OpenSSL在很多领域都少有记录。比特币寻址和密钥对的储存本可以更加高效，代码已经被更新来确保这种情况。

安全一直是一种风险函数而不是一种绝对。

声明：此文出于传递更多信息之目的，并不意味着赞同其观点或证实其描述。本网站所提供的信息，只供参考之用。